日常备忘记录

1. Python 字符串前加u,r,b的含义

  • 字符串前加u

    后面字符串以 Unicode 格式 进行编码，一般用在中文字符串前面（例：u”我是含有中文字符组成的字符串。”）

  • 字符串前加r

    去掉反斜杠的转义机制。（例：r”\n\n\n\n”　　# 表示一个普通生字符串 \n\n\n\n，而不表示换行了。）

  • 字符串前加b

    表示后面字符串是bytes 类型。

2. Pytorch item()方法

  • 返回这个张量的值作为标准Python值。这只适用于只有一个元素的张量。(一般损失都用这个方法，loss.item())
1
2
3
>>> x = torch.tensor([1.0])
>>> x.item()
1.0

3. Pytorch view()和reshape()区别

相同点：都是将原张量元素重组为新的shape

不同点：reshape()限制更小，只要满足重组前后包含元素相同即可。view()有一些限制，例如，当tensor经过transpose()操作后，改变了tensor中的元素（比如交换了元素的位置），但是tensor在内存空间中的存储位置没有改变，那么变换后的tensor在内存空间中的存储就不连续了。此时view()方法不能直接使用。需要先调用contiguous()，使tensor的元素在内存空间中连续后，再调用view()方法。

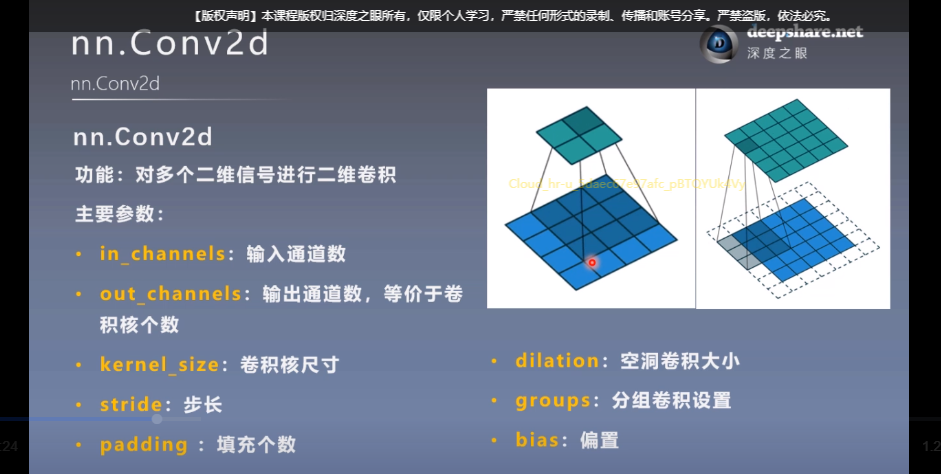
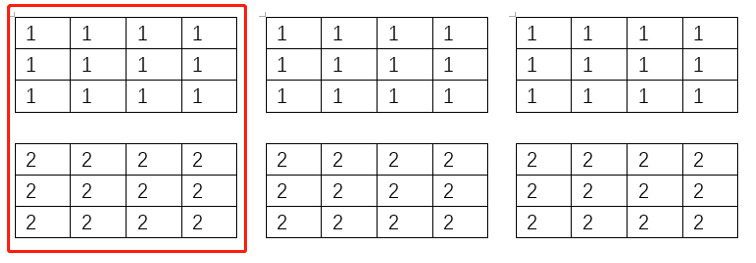
４. Pytorch Conv1d和Conv2d理解

image-20201019155955452

1
2
3
4
5
6
7
8
import torch.nn as nn
import torch

conv1 = nn.Conv1d(300, 500, 5, 2) # embedding_size, out_channels, kernel_size, stride
input = torch.ones((32, 300, 10))  # batch_size, embedding_size, length
print(input)
out = conv1(input)
print(out)

注：kernel_size表示卷积核（过滤器）的大小，而filters表示过滤器的数量

Conv2d

image-20201021092815815

5.神经网络不能求导的情况

网络不能求导的操作就是sample, 在sample的时候，可能是一个直接的概率分布，比如各个动作的概率，或者是一个概率分布的参数，比如VAE， 而造成不能求导的原因是输入和输出数据之间的直接关联性被打破，输入数据的变化，不能立马反映在输出结果上。即不是 continous operation.

只要是网络的操作固定，比如max pooling这样的，不管输入的数据怎么随机变化，总是有一个确定性的选择的过程。而sample是不行的，sample是对于一个概率分布的采用，采样的结果，和描述概率分布或者描述概率分布的参数之间没有直接对应的关系，感觉是这种没有直接对应关系的现状造成了不能求导，换句话说，输入和输出直接没有直接关系。但是max pooling这样的操作实际上是在输入数据集合里面做选择，输入数据和输出数据是具有直接关系的，即改变输入的值，能立马影响输出的值。而sample的话是不行的。

6.重参数技巧

sample操作会导致网络无法反向传播求导，因此重参数技巧就是为了解决该问题。

image-20201020111850009

新的见解：Gumbel Softmax解决了两个问题，1）采样不均。2）梯度不可导。第一点通过添加Gumbel分布中采样的随机噪声。第二点则利用Softmax替代one_hot+argmax（已经证明，Gumbel Softmax可以等价于one_hot+argmax，当退火参数很小时）。对于梯度不可导这点，还有一种解决方法，通过利用强化学习的策略梯度。

image-20230516211817752

通过以上操作，$\epsilon$控制随机性，而整体项可以反向传播求导。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class GumbelSoftmax(Layer):
    """Gumbel Softmax重参数
    """
    def __init__(self, tau=1., **kwargs):
        super(GumbelSoftmax, self).__init__(**kwargs)
        self.tau = K.variable(tau)
    def call(self, inputs):
        epsilon = K.random_uniform(shape=K.shape(inputs))
        epsilon = - K.log(epsilon + K.epsilon())
        epsilon = - K.log(epsilon + K.epsilon())
        outputs = inputs + epsilon
        outputs = K.softmax(outputs / self.tau, -1)
        return outputs

gumbel_softmax = GumbelSoftmax()
z_sample = gumbel_softmax(logits) # logits:神经网络的输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
def onehot_from_logits(logits, eps=0.0):
    """
    Given batch of logits, return one-hot sample using epsilon greedy strategy
    (based on given epsilon)
    """
    # get best (according to current policy) actions in one-hot form
    argmax_acs = (logits == logits.max(1, keepdim=True)[0]).float()
    #print(logits[0],"a")
    #print(len(argmax_acs),argmax_acs[0])
    if eps == 0.0:
        return argmax_acs

# modified for PyTorch from https://github.com/ericjang/gumbel-softmax/blob/master/Categorical%20VAE.ipynb
def sample_gumbel(shape, eps=1e-20, tens_type=torch.FloatTensor):
    """Sample from Gumbel(0, 1)"""
    U = Variable(tens_type(*shape).uniform_(), requires_grad=False)
    return -torch.log(-torch.log(U + eps) + eps)

# modified for PyTorch from https://github.com/ericjang/gumbel-softmax/blob/master/Categorical%20VAE.ipynb
def gumbel_softmax_sample(logits, temperature):
    """ Draw a sample from the Gumbel-Softmax distribution"""
    y = logits + sample_gumbel(logits.shape, tens_type=type(logits.data))
    return F.softmax(y / temperature, dim=1)

# modified for PyTorch from https://github.com/ericjang/gumbel-softmax/blob/master/Categorical%20VAE.ipynb
def gumbel_softmax(logits, temperature=1.0, hard=False):
    """Sample from the Gumbel-Softmax distribution and optionally discretize.
    Args:
      logits: [batch_size, n_class] unnormalized log-probs
      temperature: non-negative scalar
      hard: if True, take argmax, but differentiate w.r.t. soft sample y
    Returns:
      [batch_size, n_class] sample from the Gumbel-Softmax distribution.
      If hard=True, then the returned sample will be one-hot, otherwise it will
      be a probabilitiy distribution that sums to 1 across classes
    """
    y = gumbel_softmax_sample(logits, temperature)
    if hard:
        y_hard = onehot_from_logits(y)
        #print(y_hard[0], "random")
        y = (y_hard - y).detach() + y # pytorch中通过简单的加减实现了重参数技巧
    return y

6. 论文中不定冠词和定冠词的使用情况

image-20201029161249324

7.python __getitme__(self,key)方法

凡是在类中定义了这个__getitem(self,key)__方法，那么它的实例对象（假定为p），可以像这样

p[key] 取值，当实例对象做p[key] 运算时，会调用类中的方法__getitem__(self,key)

一般如果想使用索引访问元素时，就可以在类中定义这个方法（__getitem__(self, key) ）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Test:
    def __init__(self,key,value):
        self.key = key
        self.value = value
        self.d = {self.key:self.value}
    def __getitem__(self,key):
        return self.d.get(key,"default")


t = Test(0,"123")
print(t[0])
>>>default
print(t[1])
>>>123

8. 指示函数

image-20201110220908634

9. python yield

它首先是个return，普通的return是什么意思，就是在程序中返回某个值，返回之后程序就不再往下运行了。看做return之后再把它看做一个是生成器（generator）的一部分（带yield的函数才是真正的迭代器）

1
2
3
4
5
6
7
8
9
10
11
def foo():
    print("staring...")
    while True:
        res = yield 4
        print("res: ", res)


g = foo()  # 返回一个生成器
print(next(g))
print("*"*40)
print(next(g))
1
2
3
4
5
staring...
4
****************************************
res:  None
4

运行顺序：

1）因为foo()函数中有yield关键字，所以foo()函数不会执行，而是先得到一个生成器g

2）调用next()函数后，执行fool()函数，因此首先输出staring。当程序执行到yield时，类似于return，程序直接将4作为返回值，因此4是print(next(g))的输出

3）执行print("*"*40)

4）再次调用next()时，程序直接从res=yield 4开始执行。由于res并没有被赋值（等号右边的值已经被return了），因此print("res: ",res)输出为None

5）由于是wile True，因此程序继续执行，执行到yield 4时，类似于return，程序直接将4作为返回值，因此输出4

10. python 匿名函数

正常函数

1
2
def f1(ar1, ar2):
	return ar1 + ar2

匿名函数

1
f1 = lambda ar1,ar2: ar1 + ar2

11. python zip()

zip() 函数用于将可迭代的对象作为参数，将对象中对应的元素打包成一个个元组，然后返回由这些元组组成的列表。

如果各个迭代器的元素个数不一致，则返回列表长度与最短的对象相同

1
2
3
4
5
a = [1, 2, 3]
b = [4, 5, 6]
zipped = zip(a, b)
# print([i for i in zipped])
print(list(zipped))
1
[(1, 4), (2, 5), (3, 6)]

利用*号操作符，可以将元组解压为列表。

1
print([i for i in zip(*zipped)])
1
[(1, 2, 3), (4, 5, 6)]

12. python 迭代器输出问题

在print()输出函数下，迭代器只能输出一次。通过移动指针来消耗一个缓冲区，随时读取。如果已经读过一次，那么指针就在缓冲区的末尾，读取到的就是空的。

1
2
print([i for i in zip(*zipped)])
print([i for i in zip(*zipped)])
1
2
[(1, 2, 3), (4, 5, 6)]
[]
1
2
3
z = list(zip(*zipped))
print([i for i in z])
print([i for i in z])
1
2
3
4
(1, 2, 3)
(4, 5, 6)
(1, 2, 3)
(4, 5, 6)

13. numpy range()和arange()区别

range(start, end, step)，返回一个range.object（迭代值），起始值为start，终止值为end，但不含终止值，步长为step。只能创建int型list。

这是一个通用的函数来创建包含算术级数的列表。它最常用于for循环。参数必须是纯整数。
如果省略step参数，则默认为1。如果省略start参数，则默认为0。
完整的形式返回一个普通整数列表。
如果step是正数，最后一个元素是小于停止的最大元素; 如果step是负数，最后一个元素是大于stop的最小元素; 步骤step不能为零（否则报错）。

1
2
3
4
a = range(1,5,2)
print(list(a),type(a))
a= range(2)
print(list(a),type(a))
1
2
[1, 3] <class 'range'>
[0, 1] <class 'range'>

np.arange(start, end, step)，与range()类似，也不含终止值，但是返回一个array对象。需要导入numpy模块（import numpy as np或者from numpy import*)，并且arange可以使用float型数据。

在半开区间[start， stop）内产生值 （换句话说，包括开始但不包括停止的区间）。对于整数参数，该函数等同于Python内置的范围函数，但返回一个ndarray而不是一个列表。

1
2
3
4
5
6
7
8
import numpy as np

a = np.arange(1, 5, 2)
print(a, type(a))
a = np.arange(2)
print(a, type(a))
a = np.arange(1.1, 5.1, 2)
print(a, type(a))
1
2
3
[1 3] <class 'numpy.ndarray'>
[0 1] <class 'numpy.ndarray'>
[1.1 3.1] <class 'numpy.ndarray'>

14. python Iterable(可迭代的)对象，Iterator(迭代器)

  • 凡是可作用于for循环的对象都是Iterable类型；
  • 凡是可作用于next()函数的对象都是Iterator类型，它们表示一个惰性计算的序列；
  • 集合数据类型如list、dict、str等是Iterable但不是Iterator，不过可以通过iter()函数获得一个Iterator对象。

15. pytorch expand()和repeat()

  • expand()：扩展（expand）张量不会分配新的内存，只是在存在的张量上将一个大小（size）等于1的维度扩展到更大的尺寸。扩展维度必须与张量维度一致，并且只能扩展size为1的维度。
1
2
3
4
5
6
7
8
9
10
import torch

a = torch.ones(size=(2,3,1))
b = b.expand(-1,-1,3)
print(b.size())
c = a.expand(2,3,3)
print(c.size())
print(a)
print(b)
print(c)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
torch.Size([2, 3, 3])
torch.Size([2, 3, 3])
tensor([[[-0.7531],
         [-0.3914],
         [ 1.8335]],

        [[-0.5702],
         [-0.0542],
         [-0.2949]]])
tensor([[[-0.7531, -0.7531, -0.7531],
         [-0.3914, -0.3914, -0.3914],
         [ 1.8335,  1.8335,  1.8335]],

        [[-0.5702, -0.5702, -0.5702],
         [-0.0542, -0.0542, -0.0542],
         [-0.2949, -0.2949, -0.2949]]])
tensor([[[-0.7531, -0.7531, -0.7531],
         [-0.3914, -0.3914, -0.3914],
         [ 1.8335,  1.8335,  1.8335]],

        [[-0.5702, -0.5702, -0.5702],
         [-0.0542, -0.0542, -0.0542],
         [-0.2949, -0.2949, -0.2949]]])
  • repeat(): 重复，沿着特定的维度重复这个张量。得到的张量size=原始张量size*重复size
1
2
3
4
5
6
7
8
9
10
import torch

a = torch.randn(size=(2,3))
b = a.repeat(1,2)
c = a.repeat(2,2)
print(b.size())
print(c.size())
print(a)
print(b)
print(c)
1
2
3
4
5
6
7
8
9
10
torch.Size([2, 6])
torch.Size([4, 6])
tensor([[-1.0002, -1.3370,  0.3203],
        [-0.4647, -1.8016, -0.3442]])
tensor([[-1.0002, -1.3370,  0.3203, -1.0002, -1.3370,  0.3203],
        [-0.4647, -1.8016, -0.3442, -0.4647, -1.8016, -0.3442]])
tensor([[-1.0002, -1.3370,  0.3203, -1.0002, -1.3370,  0.3203],
        [-0.4647, -1.8016, -0.3442, -0.4647, -1.8016, -0.3442],
        [-1.0002, -1.3370,  0.3203, -1.0002, -1.3370,  0.3203],
        [-0.4647, -1.8016, -0.3442, -0.4647, -1.8016, -0.3442]])

16. python extend()，append()

  • extend()：在列表末尾一次性追加另一个序列中的多个值
  • append(): 在列表末尾添加新的对象
1
2
3
4
5
6
a = [1, 2, 3]
b = a.copy()
a.extend([4, 5, 6])
print(a)
b.append([4, 5, 6])
print(b)
1
2
[1, 2, 3, 4, 5, 6]
[1, 2, 3, [4, 5, 6]]

17. pytorch stack()

1
2
torch.stack(tensor:连接的张量序列,
			dim=0)
1
2
3
4
5
6
7
import torch
a = torch.tensor([[1, 2, 3], [4, 5, 6]])
b = torch.tensor([[7, 8, 9], [10, 11, 12]])
c0 = torch.stack([a, b], dim=0)
c1 = torch.stack([a, b], dim=1)
print(c0)
print(c1)
1
2
3
4
5
6
7
8
9
10
tensor([[[ 1,  2,  3],
         [ 4,  5,  6]],

        [[ 7,  8,  9],
         [10, 11, 12]]])
tensor([[[ 1,  2,  3],
         [ 7,  8,  9]],

        [[ 4,  5,  6],
         [10, 11, 12]]])

  • dim=0时， c = [ a, b]

  • dim=1时， d = [ [a[0] , b[0] ] , [a[1], b[1] ] ]

  • dim=2时， e = [ [ [ a[0] [0], b[0] [0] ] , [ a[0] [1], b[0] [1] ] , [ a[0] [2],b[0] [2] ] ] ,

    ​ [ [ a[1] [0], b[1] [0] ] , [ a[1] [1], b[0] [1] ] , [ a[1] [2],b[1] [2] ] ] ]

18. pytorch nn.LayerNorm()

1
2
3
4
torch.nn.LayerNorm(
        normalized_shape: Union[int, List[int], torch.Size],
        eps: float = 1e-05,
        elementwise_affine: bool = True)

公式：$y=\frac{x-E[x]}{\sqrt{Var[x]+\epsilon}}*\gamma+\beta$

​ $E[x]=\frac{\sum_{i=1}^nx_i}{n}$

​ $Var[x]=\sqrt{\frac{\sum_{i=1}^n(x_i-E[x])^2}{n}}$

  • $E[x]$均值和$Var[x]$方差分别在最后几个维度计算，这些维度是由normalized_shape指定。

  • 如果elementwise_affine=True，即开启仿射变换，则$\gamma$（初值是[1.,1., …]），$\beta$(初值是[0.,0., …])加入计算。这两个变量会在反向传播时得到更新。反之，则不加入计算中，即只做归一化操作，不会进行放射变换。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import torch
import torch.nn as nn

batch_size = 3
num_features = 2
features_shape = (3, 4)

feature_map = torch.ones(features_shape)  # 2D
feature_maps = torch.stack([feature_map * (i + 1) for i in range(num_features)], dim=0)  # 3D
feature_maps_bs = torch.stack([feature_maps for i in range(batch_size)], dim=0)  # 4D

ln = nn.LayerNorm(feature_maps_bs.size()[1:], elementwise_affine=True)

output = ln(feature_maps_bs)

print("Layer Normalization")
print(feature_maps_bs.shape)
print(ln.weight.shape)
print(feature_maps_bs[0, ...])
print(output[0, ...])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Layer Normalization
torch.Size([3, 2, 3, 4])
torch.Size([2, 3, 4])
tensor([[[1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.]],

        [[2., 2., 2., 2.],
         [2., 2., 2., 2.],
         [2., 2., 2., 2.]]])
tensor([[[-1.0000, -1.0000, -1.0000, -1.0000],
         [-1.0000, -1.0000, -1.0000, -1.0000],
         [-1.0000, -1.0000, -1.0000, -1.0000]],

        [[ 1.0000,  1.0000,  1.0000,  1.0000],
         [ 1.0000,  1.0000,  1.0000,  1.0000],
         [ 1.0000,  1.0000,  1.0000,  1.0000]]], grad_fn=<SelectBackward>)

image-20201202102053493

​ $E[x]=1.5,Var[x]=(0.5)^2$

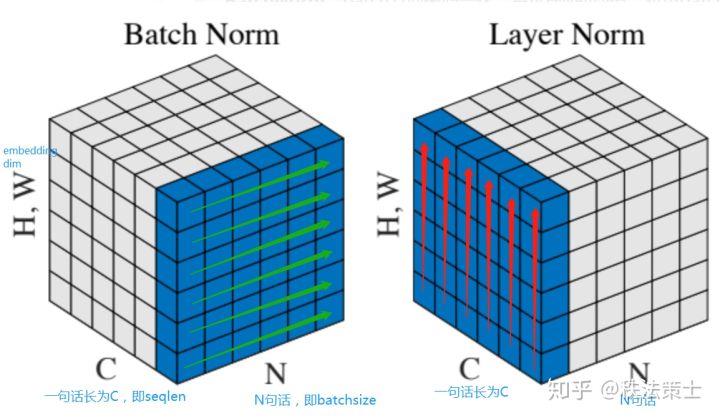
19. Pytorch 详解BatchNorm和LayerNorm差别

图像：(N,C,H,W) N表示batch_size，C表示通道数量，H表示图像的高，W表示图像的宽

文本：(N,C,H,W) N表示batch_size，C表示seq_len，H,W表示embedding_size

BN

BatchNorm是在(N)batch_size维度上进行归一标准化操作。从图中可以看出，BatchNorm是将一个Batch中的每一个文本的每一个词（图中可以理解为第一个词）的词向量的第一个维度进行归一标准化。由于一个Batch中文本的长度不一定相同，会有很多的文本中有padding，从而导致影响归一标准化的精确度。因此，BatchNorm不太适合与文本。

LayerNorm是在(H,W)embedding_size维度上进行归一标准化操作。从图中可以看出，LayerNorm是将文本中的每一个词的词向量进行归一标准化。不难发现，它并不受Batch的影响，其操作其实就是实施在神经网络的一层上，因此被称为LayerNorm。

20. python strip()

strip()用于移除字符串头尾指定的字符或字符序列

1
str.strip([chars])
1
2
3
4
5
6
7
8
a = 'aThis is an apple .a'
print(a.strip('a'))  # remove 'a'
b = ' This is an apple .'
print(b.strip())  # remove space
c = ' This is an apple .'
print(c.strip('This'))
d = 'This is an apple .'
print(d.strip('This'))  # remove 'This'
1
2
3
4
This is an apple .
This is an apple .
 This is an apple .
 is an apple .

21. 标准差（SD）和标准误差（SE）

方差：$s^2=\frac{\sum_{i=1}^n(x_i-E[x])^2}{n}$

SD：$\sigma=\sqrt{\frac{\sum_{i=1}^n(x_i-E[x])^2}{n}}$

SE：$\sigma_n=\frac{\sigma}{\sqrt{n}}$

标准差表示样本数据的离散程度。

标准误差表示抽样的误差（精密度）。

22. 验证集作用

作用：为了调整超参数

来源：从训练集中采样

模型训练、测试完整过程：

img

例子：当数据集比较小时，采用交叉验证方法可以“充分利用”有限的数据，找到合适的模型参数，防止过拟合

作用：数据集小时防止过拟合。找到合适模型参数。

方法：将数据集分成N份，将N-1份作为训练集，剩余1份作为验证集。使用以上N种情况的训练集训练模型得到模型的参数。

结果：依据损失函数选择最优模型和参数。

23. Pytorch的dim理解

只有dim指定的维度是可变的，其他维度都是固定不变的
dim = 0，指定的是行，那就是行变，列不变，理解成：同一列中每一行之间的比较或者操作

例子：

1）torch.argmax()：得到最大值的序号索引

1
2
3
4
5
6
a = torch.rand((3, 4))
print(a)
b = torch.argmax(a, dim=1)  # 指定列，也就是行不变，列之间的比较
print(b)
c = torch.argmax(a, dim=0)  # 指定行，也就是列不变，行之间的比较
print(c)
1
2
3
4
5
tensor([[0.0321, 0.0604, 0.8718, 0.0475],
        [0.0723, 0.9482, 0.3159, 0.4461],
        [0.4151, 0.7802, 0.7472, 0.5297]])
tensor([2, 1, 1])
tensor([2, 1, 0, 2])

2）torch.sum()：求和

1
2
3
4
5
a = torch.arange(0, 6).view(2, 3)
print(a)
print(a.sum())
print(a.sum(dim=0))  # 指定行，列不变，行之间求和
print(a.sum(dim=1))  # 指定列，行不变，列之间求和
1
2
3
4
5
tensor([[0, 1, 2],
        [3, 4, 5]])
tensor(15)
tensor([3, 5, 7])
tensor([ 3, 12])

3）torch.cumsum()：累加

1
2
3
4
a = torch.arange(0, 6).view(2, 3)
print(a)
print(a.cumsum(dim=0))  # 指定行，列不变，行进行操作，从第一行到最后一行的累加
print(a.cumsum(dim=1))  # 指定列，行不变，列进行操作，从第一列到最后一列的累加
1
2
3
4
5
6
tensor([[0, 1, 2],
        [3, 4, 5]])
tensor([[0, 1, 2],
        [3, 5, 7]])
tensor([[ 0,  1,  3],
        [ 3,  7, 12]])

24. Pytorch的*,matmul,mm,bmm

矩阵A，B， A*B，即点乘(dot)，要求矩阵A，B的维度必须相同
张量A，B，torch.matmul(A,B)，即张量乘法（支持高维Tensor），要求张量A的最后一个维度与张量B的第一个维度必须相同
矩阵A，B，torch.mm(A,B)，即矩阵乘法（只支持二维Tensor），要求矩阵A的列与矩阵B的行维度必须相同
张量A，B，torch.bmm(A,B)，即张量乘法（只支持三维Tensor），要求张量A的最后维度与矩阵B的第一维度必须相同。一般A，B的第一维度为batch_size

例子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
a_23 = torch.arange(0, 6).view(2, 3).type(torch.LongTensor)
a_batch_123 = torch.arange(0,6).view(1,2,3).type(torch.LongTensor)
b_32 = torch.ones((3, 2)).type(torch.LongTensor)
b_23 = torch.ones((2, 3)).type(torch.LongTensor)
b_batch_132 = torch.ones((1,3,2)).type(torch.LongTensor)

# dot, ma, mm, bmm
dot = a_23 * b_23
ma = torch.matmul(a_23, b_32)
mm = torch.mm(a_23, b_32)
bmm = torch.bmm(a_batch_123, b_batch_132)

print("a_23 ", a_23)
print("b_32 ", b_32)
print("b_23 ", b_23)
print("dot ", dot)
print("matmul ", ma)
print("mm ", mm)
print("bmm ", bmm)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
a_23  tensor([[0, 1, 2],
        [3, 4, 5]])
b_32  tensor([[1, 1],
        [1, 1],
        [1, 1]])
b_23  tensor([[1, 1, 1],
        [1, 1, 1]])
dot  tensor([[0, 1, 2],
        [3, 4, 5]])
matmul  tensor([[ 3,  3],
        [12, 12]])
mm  tensor([[ 3,  3],
        [12, 12]])
bmm  tensor([[[ 3,  3],
         [12, 12]]])

25.下载Huggingface 的预训练模型并进行加载

这里以加载Bert-based-uncased （忽略大小写信息，所有文本都转为小写）模型为例，通过[链接]: https://huggingface.co/bert-base-uncased下载预训练模型（下载三个文件`config.json`, pytorch_model.bin,vocab.txt），并将下载好的文件存储到本地，然后通过下方代码即可加载Ber模型。

1
2
3
4
5
6
7
8
9
10
11
from transformers import BertModel, BertTokenizer

model_name = '路径\\bert_based_uncased'
tokenizer = BertTokenizer.from_pretrained(model_name,do_lower_case=True)
model = BertModel.from_pretrained(model_name,  return_dict=True)
model.eval()
inputs = tokenizer("the", return_tensors="pt")
outputs = model(**inputs)

last_hidden_states = outputs.last_hidden_state
print(last_hidden_states.size()) # [batch_size, seq_len, hidden_dim]  [1,3,768]

15.ubuntu下切换cuda版本